The unit-0 review week gave me a chance to finally tackle a project I’ve been wanting to work on for a while: a Processing sketch of Conway’s Game of Life. Here’s a .gif of the sketch running an R-pentomino visualization:
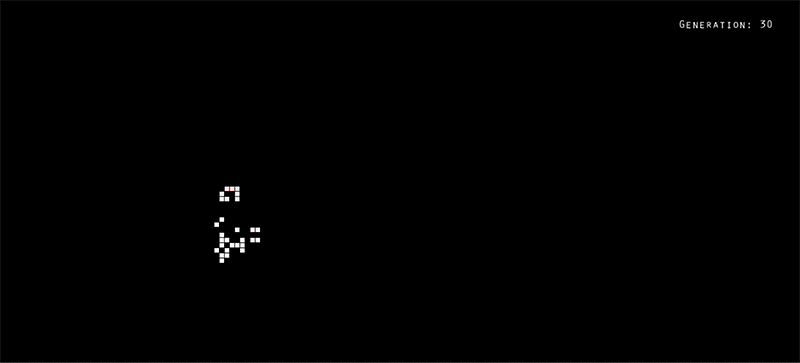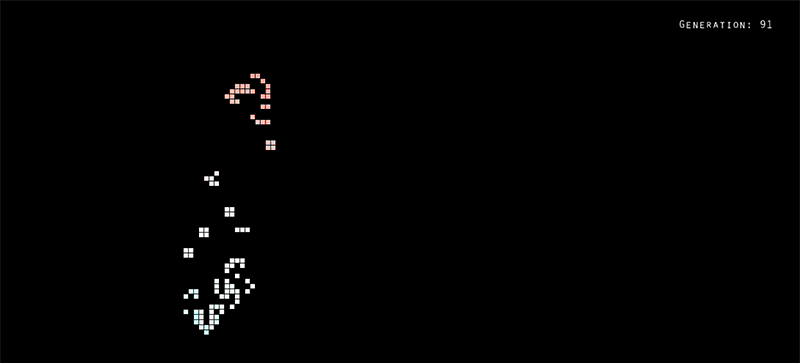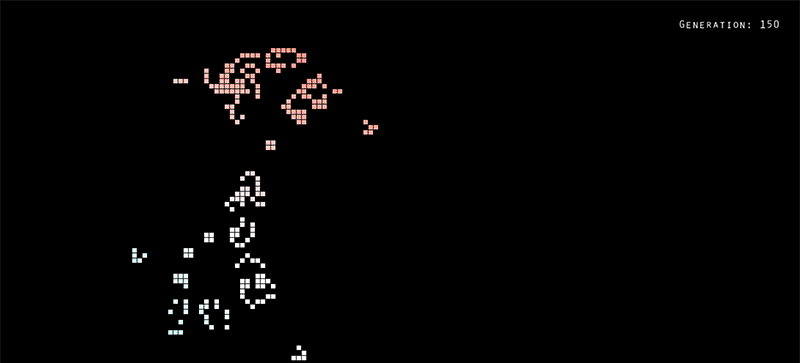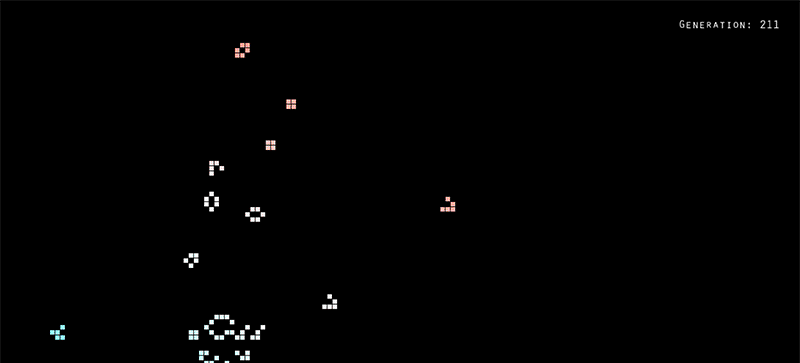
Conway’s Game of Life is a cellular automaton that was conceived in 1970 by John Conway, a British mathematician. The idea is pretty simple: a two-dimensional space is divided up into a grid of square cells. Each cell has two possible states: live or dead. Each cell is aware of its eight neighbors (the cells which are directly or diagonally adjacent). The game steps forward in generations, and with each new generation:
- Any live cell with less than two live neighbors dies (under-population).
- Any live cell with two or three live neighbors lives on.
- Any live cell with more than three live neighbors dies (overcrowding).
- Any dead cell with exactly three live neighbors becomes live.
The game must be populated with a ‘seed’: an initial state of live and dead cells from which subsequent generations can evolve. This is where things get interesting.
Once I figured out code for the game’s logic and got the Processing applet running, I started to explore some of the incredible seed patterns that have been discovered. Patterns are available on the internet as .lif files, which are essentially (x, y) coordinate sets indicating live cells. I wrote a method to parse these files so that I could easily download and try out new patterns.